Область определения функций
Сегодня мы рассмотрим понятие области определения функции.
Понятие области определения функции
Впервые школьники сталкиваются с понятием "функция" на уроках алгебры в седьмом классе, и с каждой новой четвертью, с каждой новой темой, это понятие раскрывается с новых сторон, а задачи становятся более сложными. Сегодня мы дадим определения ключевым терминам и научимся определять область определения функции, заданной формулой или графически.
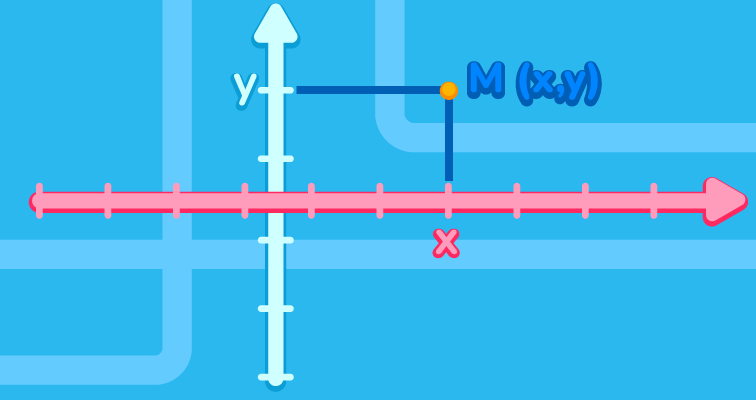
Если каждому значению переменной x из определенного множества соответствует число y, это означает, что на этом множестве определена функция. При этом переменную x называют независимой переменной или аргументом, а переменную y - зависимой переменной или значением функции.
Зависимость переменной y от переменной x называется функциональной зависимостью и обозначается как y = f(x).
Что такое функция и её область определения?
Функция - это соответствие между двумя множествами, при котором каждому элементу первого множества соответствует один элемент второго множества.
Исходя из определения функции, мы можем сформулировать определение области определения функции.
Область определения функции - это множество всех значений аргумента (переменной x). Геометрически это можно представить как проекцию графика функции на ось Ox. Область определения некоторой функции обычно обозначается как D(y).
Множество значений функции - это множество всех значений, которые функция может принимать на своей области определения. Геометрически это можно представить как проекцию графика функции на ось Oy.
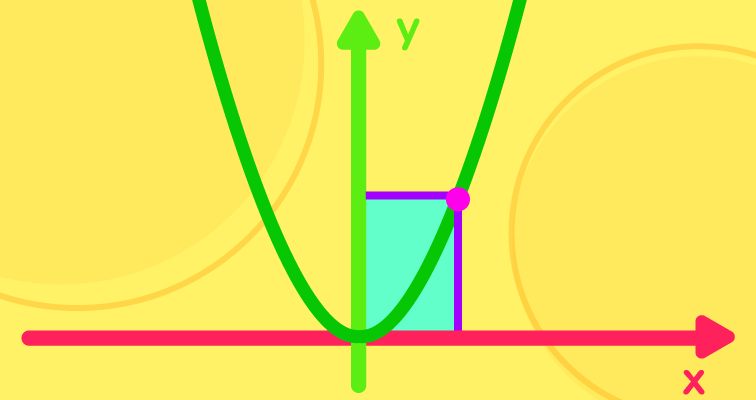
Давайте рассмотрим пример: область значений функции y = x^2 - это все числа, большие или равные нулю. Это можно записать следующим образом: D(y): y ≥ 0.
Чтобы описать область определения функции словами, часто приходится использовать громоздкие описания. Поэтому мы используем специальные символы и обозначения.
Если мы хотим указать диапазон чисел, мы поступаем следующим образом:
• Через точку с запятой мы указываем левую и правую границы диапазона.
• Если граница включается в диапазон, мы используем квадратную скобку рядом с ней, если не включается - круглую скобку.
• Если диапазон не имеет правой границы, мы записываем +∞. Если нет левой границы, мы пишем -∞.
• Если нам нужно объединить несколько диапазонов, мы используем символ объединения: ∪.
Область определения линейной функции
Линейная функция задается формулой y = ax + b, где a и b - константы. Область определения линейной функции - множество всех действительных чисел R. Это связано с тем, что линейная функция не имеет ограничений на значения аргумента x.
Область определения квадратичной функции
Квадратичная функция имеет вид y = ax^2 + bx + c, где a, b и c - константы. Область определения квадратичной функции также является множеством всех действительных чисел R, так как она не имеет ограничений на значения аргумента x.
Область определения показательной функции
Показательная функция задается формулой y = a^x, где a - положительное число, не равное 1. Область определения показательной функции - множество всех действительных чисел R. Это связано с тем, что показательная функция может принимать значения для всех действительных чисел в качестве аргумента.
Область определения логарифмической функции
Логарифмическая функция имеет вид y = log_a(x), где a - положительное число, не равное 1. Область определения логарифмической функции также состоит из всех положительных действительных чисел, то есть D(log_a) = (0, +∞).
В заключение, область определения функции играет важную роль в математике, так как она определяет, для каких значений аргумента функция определена и может быть использована. Разбираясь в областях определения различных элементарных функций, студенты приобретают навыки анализа и понимания поведения функций в разных математических задачах.
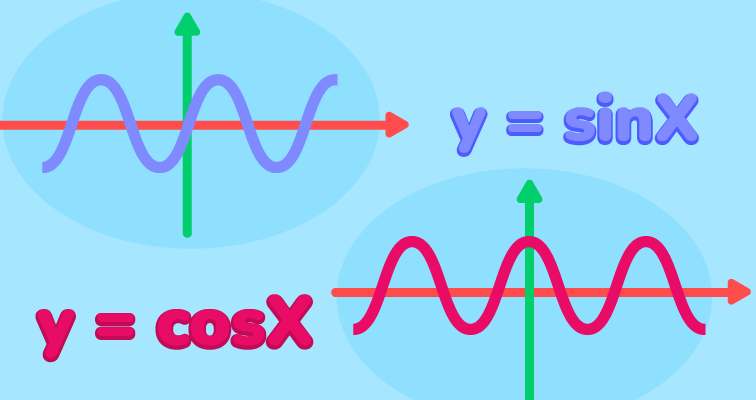
Область определения тригонометрических функций
Давайте вспомним, как определяются их области определения и разберем примеры.
1. Синус (sinx): Эта функция определена на всем множестве действительных чисел, обозначается как sin, и ее область определения равна множеству всех действительных чисел, т.е., D(sin) = R.
2. Косинус (cosx): Косинус тоже определен на всем множестве действительных чисел, обозначается как cos, и его область определения также равна множеству всех действительных чисел, т.е., D(cos) = R.
3. Тангенс (tgx): Тангенс определен на всем множестве действительных чисел, за исключением точек, где косинус равен нулю, т.е., x ≠ π/2 + πk, где k - целое число. Область определения тангенса: D(tg) = R, x ≠ π/2 + πk.
4. Котангенс (ctgx): Котангенс, как и тангенс, определен на всем множестве действительных чисел, за исключением точек, где синус равен нулю, т.е., x ≠ πk, где k - целое число. Область определения котангенса: D(ctg) = R, x ≠ πk.
Пример:
Пусть нам нужно найти область определения функции f(x) = tg(2x).
Как решаем:
Так как a(x) = 2x, то мы не можем включать точки, где тангенс становится бесконечным (это происходит, когда косинус равен нулю). Такие точки можно найти, решив уравнение cos(2x) = 0:
cos(2x) = 0
Для этого мы можем найти все значения x, при которых cos(2x) равен нулю. Это происходит, когда аргумент 2x равен π/2 + πk, где k - целое число.
2x = π/2 + πk
Теперь делим обе стороны на 2, чтобы найти значения x:
x = (π/4) + (π/2)k
Таким образом, область определения функции f(x) = tg(2x) - это множество всех действительных чисел x, за исключением точек x = (π/4) + (π/2)k, где k - целое число.
Область определения: D(f) = R, x ≠ (π/4) + (π/2)k.

Теперь вы можете понимать область определения тригонометрических функций и использовать ее для решения задач.
Читать дополнительно:

Что ребенок должен знать об окружающем мире?
Окружающий мир каждый день дает ребенку новые впечатления, но есть вещи, которым стоит научить каждого дошкольника. Что это - расскажем в Юту!
Читать статью полностью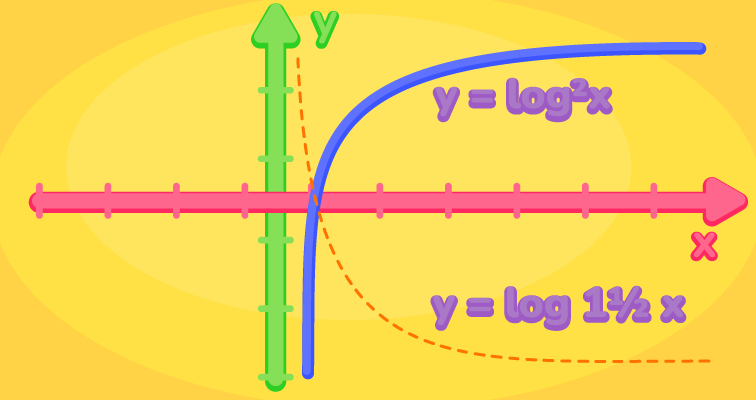
Логарифмы
Друзья, сегодня мы займемся удивительным миром логарифмов, которые приходят на помощь, когда решаем головоломки с числами.
Читать статью полностью
Таблица умножения
Как быстро и легко выучить таблицу умножения. Легко запоминаем таблицу умножения от 1 до 10, до 20. Научим ребенка умножать за день!
Читать статью полностью