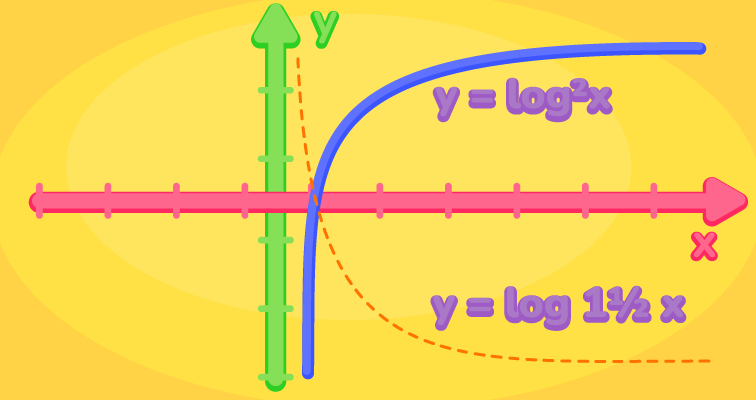
Логарифмы
Что такое логарифм?
Логарифмы помогают нам понимать, какую степень нужно возвести числа, чтобы получить другое число. Давайте разберемся.
Представьте, у нас есть число 100. И мы хотим узнать, какую степень надо возвести числа 10, чтобы получить 100. Этот логарифм обозначается как log10(100), и он равен 2, потому что 10 во второй степени равно 100.
Почему это важно?
Логарифмы полезны, когда мы работаем с огромными или маленькими числами. Они помогают упростить сложные математические задачи.
Свойства логарифмов
Логарифмы обладают некоторыми интересными свойствами:
1. Когда вы умножаете числа, логарифм их произведения равен сумме логарифмов этих чисел.
log(a * b) = log(a) + log(b)
2. Когда вы делите числа, логарифм их отношения равен разности логарифмов этих чисел.
log(a / b) = log(a) - log(b)
3. Если вы возводите число в степень, логарифм этой степени равен произведению степени и логарифма числа.
log(a^k) = k * log(a)
Как использовать логарифмы?
Логарифмы приходят на помощь, когда решаем сложные уравнения или задачи с процентами, научиться им работать — это как открыть волшебный ящик для решения сложных задач. Так что давайте погрузимся в мир логарифмов и будем волшебниками математики вместе!
Как работать с логарифмами?
Давайте сделаем логарифмы более доступными, как магические ключи к числовому миру.
Что такое логарифм?
Логарифм помогает нам узнать, в какую степень нужно возвести число, чтобы получить другое число. Давайте это проиллюстрируем.
Представьте, у нас есть число 100. Мы хотим узнать, во сколько раз нужно возвести число 7, чтобы получить 100. Этот логарифм обозначается как log₇(100), и он равен 2, потому что 7 возводим во вторую степень и получаем 100.
Для чего это полезно?
Логарифмы помогают справляться с огромными или крошечными числами и решать сложные задачи.
Основные свойства логарифмов
У логарифмов есть несколько важных свойств:
1. Умножение чисел внутри логарифма эквивалентно сложению логарифмов:
log₇(ab) = log₇(a) + log₇(b)
2. Деление чисел внутри логарифма эквивалентно вычитанию логарифмов:
log₇(a/b) = log₇(a) - log₇(b)
3. Возводление числа в степень внутри логарифма эквивалентно умножению степени и логарифма:
log₇(aⁿ) = n * log₇(a)
4. Меняя основание логарифма, мы можем перейти от одного логарифма к другому:
log₇(a) = logₓ(a) / logₓ(7)
5. Частное случаи предыдущего свойства позволяет менять местами основание и аргумент логарифма:
log₇(a) = 1 / log₇(𝑎)
Эти свойства помогают решать сложные уравнения и задачи.
Практическое применение
Логарифмы используются в самых разных областях, от точных наук до природных явлений. Они помогают моделировать спирали в галактиках, форму рогов горных козлов, усики растений и даже вращение ураганов.
